Buscas cegas são abordagens interessantes para encontrar a solução de problemas em que se conhece muito pouco sobre o problema em si. Entretanto, com o mínimo de informações possível sobre o problema que se deseja resolver é possível encontrar soluções mais eficientes.
A estratégia básica é a busca pelo primeiro melhor. Esse algoritmo é uma instância geral dos algoritmos busca em árvores ou em grafos e seleciona-se o nó para a expansão baseando-se na função de avaliação f(n). A função de avaliação é utilizada para estimar o custo, se um vértice tem a menor avaliação, então ele é expandido primeiro. A implementação da busca pelo primeiro melhor tem uma implementação idêntica à busca uniforme, exceto que esta usa uma função f ao invés de uma função g para construir a lista de prioridades. A escolha de como construir essa função de avaliação determina como será feita a busca, é comum também que esse algoritmos também inclua uma função h(n) que denota uma função heurística. “h(n) = estimated cost of the cheapest path from the state at node n to a goal state.” - Peter Norvig & Russel Stuart
Observe que a função h(n) utiliza um nó como entrada e depende apenas do estado daquele nó específico. Uma função heurística é a forma mais comum de se adicionar conhecimento e direcionar a busca de um algoritmo. Nós consideramos que uma função heurística é arbitrária, não negativa, relativa ao problema e com apenas uma restrição: se n é o nó objetivo, então h(n) = 0.
Busca Gananciosa do Melhor Primeiro (Greedy best-first search)
O algoritmo de busca gananciosa do melhor primeiro busca expandir o nó que está mais próximo do objetivo. Ou seja, utiliza uma função de avaliação que é idêntica à função heurística : f(n) = h(n).
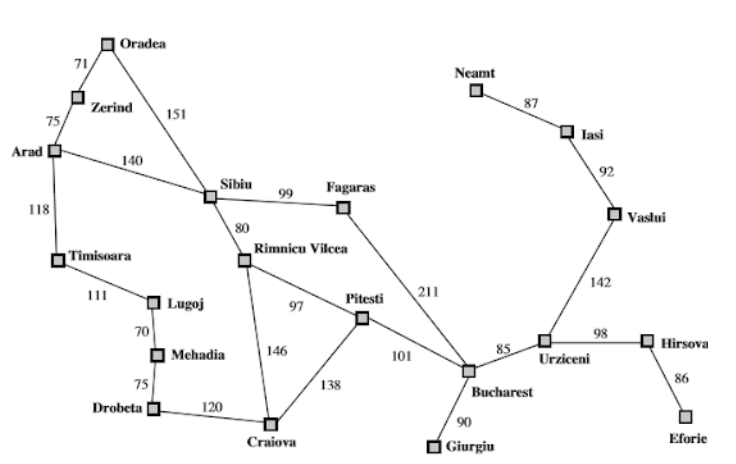
Utilizando o valor da distância em linha reta entre uma cidade e Bucharest no grafo apresentado é gerada uma função heurística hSLD apresentados na tabela a seguir:
Note que o método de busca gananciosa do melhor primeiro é incompleto se for implementado utilizando a estrutura de árvores e não de grafos, mesmo em espaços finitos, assim como a busca em profundidade. A implementação utilizando grafos resolve este problema para espaços de busca finitos. O pior caso de custo de tempo e espaço para esta árvore é de O(bm), em que m é o valor máximo da profundidade no espaço de busca. Essa é uma boa função heurística já que a complexidade da busca pode ser reduzida de maneira substancial.
Busca A* (A-Estrela / A-Star)
O algoritmo mais conhecido para busca é o A*. Ele avalia um nó através da combinação do valor de g(n), o custo até chegar em determinado nó, com h(n), a estimativa para chegar de um nó até o objetivo. f(n) = g(n) + h(n)
Como a função g(n) informa o custo do nó inicial até o nó n e h(n) informa o custo estimado deste caminho de n até o objetivo nós obtemos que f(n) é o custo estimado da solução mais barata que passa por n. Portanto, estamos buscando a solução que contenha o menor valor de g(n) + h(n). Destaca-se que o A* é uma busca tanto completa quanto ótima. O algoritmo é idêntico à busca uniforme, entretanto o A* utiliza g + h ao invés de apenas g.
- Otimização: O A* exige duas condições para ser ótimo:
- A primeira condição para que o A* seja ótimo, utilizando a implementação com árvores, é que a função heurística seja admissível. Uma função heurística admissível nunca deve superestimar o custo para chegar à um objetivo. Heurísticas admissíveis são por natureza otimistas já que consideram que o custo de solucionar um problema é menor do que realmente é. Um exemplo óbvio de função heurística é a distância entre duas cidades em linha reta como foi apresentada nos exemplos anteriores.
- A segunda condição para que o A* seja ótimo é a consistência (também conhecida como monotonicidade) e é requerida apenas para a busca utilizando a busca através em grafos. “A heuristic h(n) is consistent if, for every node n and every successor n’ of n generated by an action a, the estimated cost of reaching the goal from n is no greater than the step cost of getting to n’ plus the estimated cost of reaching the goal from n’: h(n) c(n, a, n’) + h(n)” - Peter Norvig & Stuart Russel
Ou seja, para cada nó n’ que é sucessor de n, o custo estimado (heurística) para alcançar o objetivo não é maior que o custo da etapa até chegar em n’ mais o custo estimado para atingir o objetivo. Observe que toda heurística que é consistente é admissível, mas nem toda heurística consistente necessariamente é admissível. Entretanto são raras as situações em que uma heurística é admissível, mas não consistente.
Escolha da Heurística x Representação do Mapa
A heurística escolhida determina diretamente o comportamento do A*.:
- Se o valor retornado pela heurística for 0, então apenas o custo somado g(n) está sendo considerado. Essa decisão transforma um algoritmo como o A* em uma busca uniforme comum.
- Se o valor retornado pela heurística for menor ou igual ao custo real da movimentação, então é garantido que o A* encontrará o menor caminho.
- Se h(n) for exatamente igual ao custo da movimentação de um nó até o objetivo, então o A* irá seguir sempre o melhor caminho e nunca irá expandirá qualquer outra rota. Isso na realidade não acontece sempre para todos os casos, mas é possível criar situações em que o A* se comporta de maneira perfeita.
- Se h(n) for em alguns momentos maior que o custo para se movimentar de um nó até o objetivo, então, o A* não garante que irá encontrar o melhor caminho
- Se o valor retornado pela h(n) for muito mais considerado do que o g(n), então o A* se torna a busca gananciosa pelo melhor primeiro
Essa capacidade do A* ser adaptado permite que seja feita uma troca entre o caminho “bom” e o “melhor” caminho. “A*’s ability to vary its behavior based on the heuristic and cost functions can be very useful in a game. The tradeoff between speed and accuracy can be exploited to make your game faster. For most games, you don’t really need the best path between two points. You need something that’s close. What you need may depend on what’s going on in the game, or how fast the computer is.” - Amit no site Red Blob Games
A representação interna de um um mapa influencia diretamente no desempenho dos algoritmos. Algoritmos de busca de menor caminho tendem a serem muito piores que um algoritmo linear. Ou seja, se você duplicar a distância a ser percorrida normalmente irá necessitar de mais que o dobro de recursos para encontrar o caminho. Algumas representações de mapas são mais úteis em determinados jogos do que outras, então é importante conhecer algumas representações comuns.
Grids
Uma representação comumente utilizada é a de grids com uma subdivisão interna uniforme comumente chamada de “tiles”. É comum que sejam utilizados em jogos com tiles quadrados ou ainda hexagonais.
A movimentação pode ser feita de duas maneiras utilizando a representação em grid. A primeira considera a movimentação entre os tiles e a segunda entre as bordas dos tiles.
Em jogos em que as peças/NPCs/Jogadores podem se movimentar apenas entre os centros dos tiles é comum a escolha de movimentação em tiles.
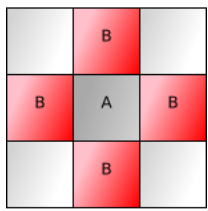
No diagrama ao lado um personagem no tile A pode se movimentar em quaisquer um dos pontos marcados por B. É possível também permitir que a movimentação seja feita na diagonal, dependendo do game design pode ser útil considerar que o custo é o mesmo ou maior dependendo do caso.
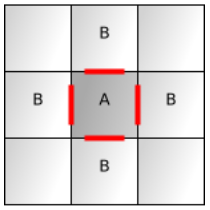
Se as unidades poderem se movimentar em qualquer local dentro da grid, ou até mesmo se os tiles são grandes, talvez seja interessante considerar que os vértices ou ainda as bordas são mais interessantes para a representação. Com o pathfinding baseado em tiles uma unidade só poderá se movimentar do centro do tile até outro, entretanto, com uma representação de bordas uma unidade poderá se movimentar diretamente entre uma borda e outra.
Distância Manhattan
Distância Manhattan é normalmente a heurística escolhida para trabalhar nesse tipo de representação. O nome dessa heurística faz uma alusão ao layout em formato de grid presente em grande parte das ruas da ilha de Manhattan. Esse formato em grid causa que o caminho mais curto feito por um carro entre duas esquinas ter a mesma distância que o caminho interno.
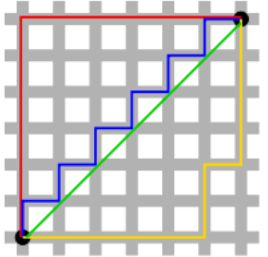
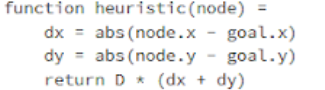
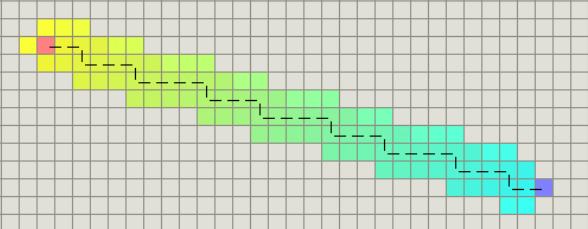
Qual o melhor valor para D? Escolha um valor que seja condizente com seu custo. Em terrenos em que o custo para se movimentar é baixo e existe uma baixa quantidade de obstáculos, mover um passo mais próximo do obstáculos deveria incrementar o custo g do caminho em D e reduzir o valor da heurística em D. Ou seja, o f é constante, pois o crescimento do custo é o mesmo que o caimento da previsão.
Distância Diagonal (Chebyshev Distance)
Se o seu mapa permite a movimentação nas diagonais, então é necessário utilizar uma outra heurística. Considere o seguinte caso: O seu personagem precisa se movimentar 4 para tiles para a direita e 4 tiles para cima (4 direita, 4 cima) e essa rota terá um custo de 8D. Entretanto, se em seu mapa é possível movimentar pela diagonal, então será interessante que o custo dessa rota seja 4D2, onde D2 é o custo de se movimentar na diagonal.
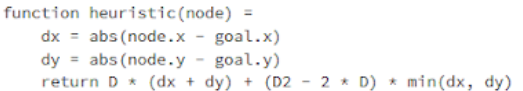
Basicamente o processo é o seguinte: Computa-se o valor dos passos que serão necessários em que não for possível andar em diagonal, então se subtrai o número de passos utilizando uma diagonal. O menor entre dx e dy equivale ao número de passos que serão feitos em diagonal e cada 1 custará D2, entretanto isso é menor que 2D.
Quando o valor de D e D2 é 1 essa heurística é chamada de distância de Chebyshev. Quando D = 1 e D2 = sqrt(2), então é a chamada de octile distance.
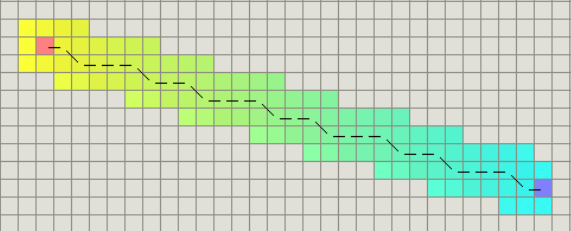
Distância Euclidiana
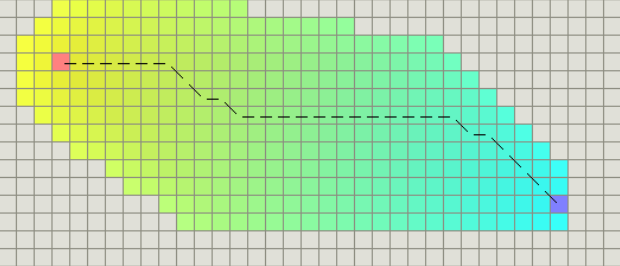
Se suas unidades podem se movimentar em qualquer ângulo, então você provavelmente poderá utilizar um cálculo de distância pura. Entretanto, com essa heurística o custo de g não irá ser idêntico ao custo de h. Como a distância euclidiana é menor que a distância Manhattan ou que a distância diagonal, então o resultado sempre será o menor caminho, entretanto o custo para rodar o A* é maior.
Mapas de Visibilidade
Uma alternativa para os mapas em grids é a utilização de uma representação com mapas de visibilidade. Se o movimento tem custo uniforme ao longo de grandes áreas e suas unidades podem se movimentar em diagonais a representação poligonal pode ser uma boa alternativa.
Considere que uma unidade deverá atravessar esse mapa entre os dois pontos indicados. O caminho mais curto será entre as bordas do obstáculos. Os cantos representam vértices que serão utilizados pelo A* ou outro algoritmo de busca.
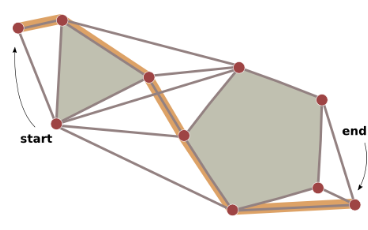Um algoritmo simples para a construção de um mapa poligonal é utilizar um algoritmo para construir mapas de visibilidade: Crie arestas entre todos os pontos que podem ser vistos entre si. Esse algoritmo é bastante simples, porém eficiente se não forem necessárias alterações desse mapa durante o jogo.
Uma busca nesse grafo é muito mais rápida que uma busca em um grafo construído em um mapa. Em um mapa sem obstáculos no caminho o A* encontrará o caminho rapidamente já que o ponto inicial e o ponto final estão conectados diretamente por uma aresta.
O problema desses mapas poligonais é crescimento dos mesmos. Em mapas de áreas abertas ou ainda em corredores longos a quantidade de arestas criadas pode se tornar impossível de ser gerenciada. Outra grande desvantagem desse método é que é necessário criar os vértices de início e fim junto com novas arestas toda vez que o A* for chamado e então remover esses nós.
NavMeshs
Ao invés de representar os obstáculos com polígonos também é possível representar a área caminhável com polígonos que não se sobrepõem. Essa área caminhável é conhecida como navigation mesh. Nessa representação, não é necessário armazenar os obstáculos presentes no ambiente. Utilizando uma navmesh o ambiente anterior pode ser representado da seguinte forma:
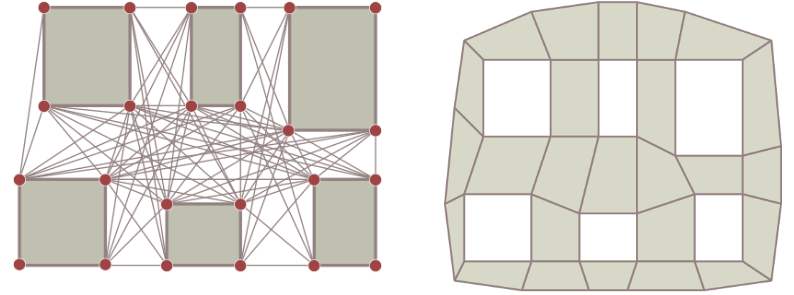
Movimentação Poligonal
Assim como em uma grid, o centro de cada polígono provê um conjunto razoável de nós que podem ser utilizados para o pathfinding. Adicionando-se o nó inicial e destino e utilizando o A* é obtido o seguinte resultado:
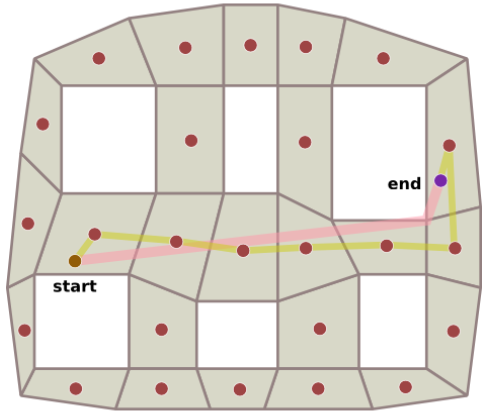
A rota rosa é o caminho ótimo, enquanto a rota amarela é o caminho encontrado pelo A* nessa situação. Observe que o caminho ideal seria o escolhido se a representação poligonal fosse a utilizada. A movimentação no centro de uma área raramente é necessária e agradável. Entretanto, é possível se movimentar através das bordas em polígonos adjacentes. Nesse exemplo foi utilizado o centro de cada uma das bordas para determinar a rota.
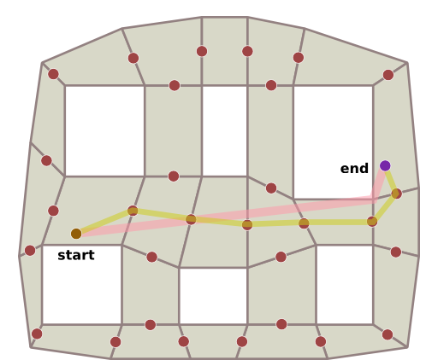
Outra abordagem possível é a utilização dos vértices dos polígonos. Entretanto essa abordagem pode acabar adicionando muitos passos e deixar uma movimentação não tão natural já que o personagem irá sempre tentar andar “colado na parede”.
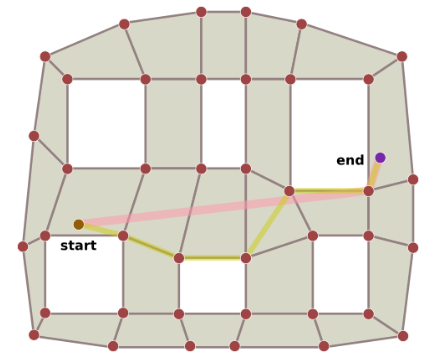
Não existem muitas regras sobre onde pode ser colocado um vértice no grafo na hora de construir uma navmesh. Então é possível combinar essas três abordagens e gerar um movimento que é um híbrido entre elas.
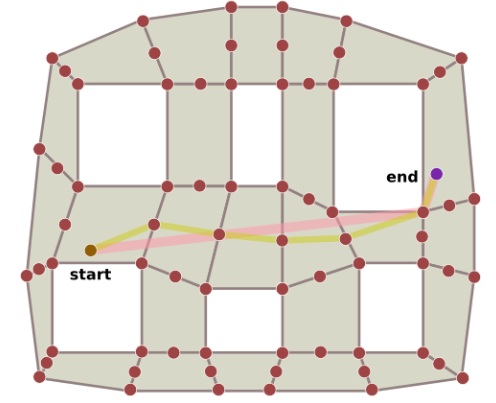
Depois de determinada um caminho é possível fazer uma suavização na rota se o custo entre todos os vértices for o mesmo. O algoritmo é bastante simples: Se existe uma linha de visão entre o vértice i e i +2, remova i + 1. Repita até que não exista mais nenhum vértice na linha de visão entre vértices adjacentes no caminho. Como resultado serão gerados apenas os vértices de navegação em torno do canto dos obstáculos, descartando assim a necessidade de utilizar os vértices da borda ou os centrais, apenas os vértices da nova rota. No exemplo anterior se a suavização de rota for utilizada, a rota amarela se tornará na rota rosa.
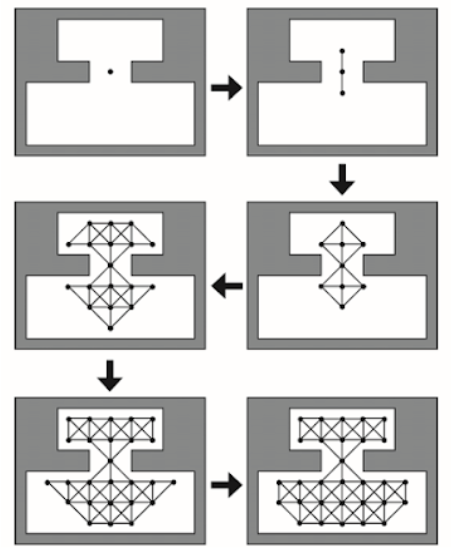
Criação de Grafos de Navegação
Para criar grafos para navegação inicialmente coloca-se um vértice em um local qualquer no mapa, comumente utiliza-se o centro do mapa. Esse algoritmo então expande os nós e as arestas para fora em todas as direções disponíveis até que toda a área navegável seja ocupada. Essa técnica é bastante similar a utilizada por programas de pintura digital com a ferramenta de preenchimento de formas irregulares (sim, o balde no paint), exceto que ao invés de preencher o mapa com uma determinada cor, esse algoritmo preenche o mapa com nós e arestas. 
｡･:*:･ﾟ★,｡･:*:･ﾟ☆ ｡･:*:･ﾟ★,｡･:*:･ﾟ☆ ｡･:*:
Contact Info:
E-mail: pamabeltrani@gmail.com
Discord: pamnawi