6. Métodos de Busca Cega

Os algoritmos de condução, as máquinas de estados e árvores de decisão são ótimos para a construção de agentes de reflexos. Entretanto, esses agentes não conseguem atuar em ambientes em que é necessário fazer um mapeamento de uma quantidade de variáveis muito grande ou ainda com algum planejamento. Para a criação de agentes orientados a objetivo é necessário considerar as ações futuras e o quão desejável é um determinado resultado.

Como apresentado anteriormente, agentes inteligentes tem como objetivo maximizar a performance em um determinado ambiente. Algumas vezes isso simplesmente pode ser simplificado se o agente pode adotar um objetivo para ser satisfeito. Objetivos ajudam a organização do comportamento e através da limitação dos objetivos possíveis que um agente deseja alcançar  é possível limitar o conjunto de ações que devem ser consideradas. Um objetivo pode ser determinado como um conjunto de estados de mundo em que o objetivo é alcançado e o objetivo de um agente é determinar como agir para alcançar esse objetivo. O primeiro passo para um agente solucionar um determinado problema, dado o estado atual do mundo, é a formulação de objetivos.  “We will consider a goal to be a set of world states - exactly those states in which the goal is satisfied. The agent’s task is to find out how to act, now and in the future, so that it reaches the goal state. Before it can do this, it need to decide (or we need to decide on its behalf) what sorts of actions and states it should consider.” - Peter Norvig & Stuart Russel em  Artificial Intelligence: A Modern Approach

O processo de formulação de problema é o processo de decisão quais ações devem ser consideradas dado um objetivo. Já o processo da busca de sequência de ações que devem ser tomadas é chamado de busca. Há duas definições de algoritmos de busca:

“A search algorithm is the step-by-step procedure used to locate specific data among a collection of data. It is considered a fundamental procedure in computing. In computer science, when searching for data, the difference between a fast application and a slower one often lies in the use of proper search algorithm”

• Technopedia

Nessa definição um algoritmo de busca em ciência da computação pode ser definido como qualquer algoritmo que resolve o problema da busca. Ou seja, um algoritmo de busca é um algoritmo que retorna uma informação guardada em uma determinada estrutura de dados, ou ainda calculado em um espaço de busca no domínio do problema. Para determinar o melhor algoritmo de busca para um determinado problema é necessário considerar a estrutura de dados utilizada nessa busca assim como qualquer conhecimento a priori disponível sobre o problema.

Outra definição possível para algoritmo de busca é a seguinte: “A search algorithm takes a problem as input and returns a solution in the form of an action sequence. Once a solution is found, the actions it recommends can be carried out. This is called the execution phase. Thus, we have a simple ‘ formulate, search, execute’ design for the agent.” - Peter Norvig & Stuart Russel em Artificial Intelligence: A Modern Approach

Utilizaremos essa definição como base nesta matéria. Utilizando essa definição é possível construir a seguinte estrutura básica do agente:

Observe que essa estrutura básica ignora as novas percepções porque considera que o resultado das ações é conhecido. Alguns conceitos são importantes para a tomada de decisão:

• Estado inicial: descreve o estado em que um agente está quando começa o planejamento. 

• Ações possíveis: Dado um estado particular s, a função ACTIONS(s) retorna o conjunto de ações que pode ser executado em s. Nós dizemos que para cada uma dessas ações é aplicável em s. 

• Modelo de transição: A descrição dos resultados obtidos por cada ação. Formalmente um modelo de transição é descrito pela função RESULT(s,a) que retorna o estado sucessor ao executar uma ação a no estado s. 

• Espaço de Busca (State Space): O conjunto de todos os possíveis estados alcançáveis dado um estado inicial por uma sequência de ações. Ao considerar o estado inicial, as ações e o modelo transição automaticamente é formado um estado espaço. Um estado espaço forma diretamente uma rede, um grafo, em que cada nó é um estado e as arestas são as ações.

• Caminho: É a sequência de estados conectados por uma sequência de ações.

• Teste de objetivo (Goal Test): Determina se um estado é um possível estado objetivo. Em alguns casos é possível explicitar quais são os estados objetivos e este teste simplesmente verifica se um dado estado está nesse conjunto.

• Custo do caminho: É função que atribui um valor numérico de custo de cada caminho. É comum a utilização de uma função que reflita o desempenho do agente. É comum assumir que o custo do caminho como a soma do custos das ações individuais ao longo do caminho.

• Solução: É a sequência de ações que levam do estado inicial até o estado objetivo. A qualidade de uma solução é determinada pelo custo de uma função e uma solução ótima tem o menor custo dentre todas as possíveis.

• Abstração: O processo de remoção de detalhes da representação.

Problemas Brinquedo x Problemas do Mundo Real

A busca pela solução de problemas é aplicada em uma grande quantidade de tarefas e ambientes. O interessante é que existe uma distinção clara entre problemas brinquedo e problemas do mundo real. Um problema brinquedo é utilizado normalmente com a intenção de ilustrar ou ainda exercitar diversas técnicas de solução de problemas. Os problemas brinquedo normalmente são utilizados por pesquisadores para comparar a performance dos algoritmos. Já problemas do mundo real acontecem no mundo real (derp). Normalmente estes são os problemas que as pessoas realmente se importam e comumente nestes problemas não existe uma única descrição.

8-puzzle

O brinquedo 8-puzzle, é um problema brinquedo, consiste de um tabuleiro 3x3 com oito números e um espaço em branco. Apenas os tiles adjacentes ao espaço em branco podem ser movidos. O objetivo final é dado um estado inicial, colocar todos os tiles na ordem correta com o espaço em branco na primeira posição da matriz.

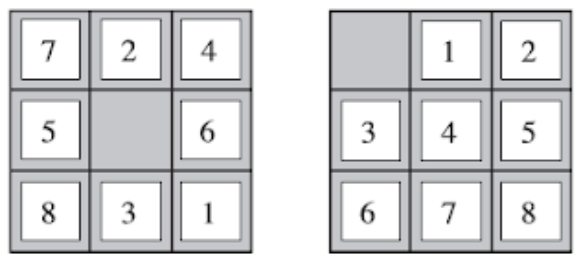
A formalização deste problema é determinada como:

• Estados: A descrição de um estado é determinada pela localização de cada um dos 8 tiles e o espaço em branco.
• Estado Inicial: Qualquer estado pode ser chamado de estado inicial. 
• Ações Possíveis: O conjunto de movimentos do espaço em branco: esquerda, direita, cima e baixo. Diferentes subconjuntos são possíveis dependendo de onde em branco está posicionado.
• Modelo de Transição: Dado o estado e a ação, este retorna o estado sucessivo. Por exemplo, se aplicarmos esquerda no estado inicial exemplo, o estado resultando conterá o 5 e o estado em branco trocados.
• Objetivo teste: Verifica se determinado estado é o estado objetivo apresentado.
• Custo do caminho: Cada passo tem um custo 1, então o custo do caminho é o número de passos necessários.

O 8-puzzle pertence a família do tipo sliding-block puzzles que são comumente utilizados para testar novos algoritmos de busca em IA. Essa família é conhecida por serem problemas do tipo NP-completo, então não é esperado para encontrar métodos significativos melhores considerando o pior caso. O 8-puzzle tem um total de 9!/2 = 181,440 estados alcançáveis e é considerado como simples de ser resolvido. O mesmo quebra-cabeça porém com uma matriz 4x4 tem em torno de 1.3 trilhões de estados alcançáveis e pode ser resolvido em apenas alguns milissegundos. Entretanto a versão 24-puzzle com uma matriz de 5x5 tem aproximadamente 1025estados e instâncias randômicas levam algumas horas para serem solucionadas de forma ótima.

Problemas P, NP e NP-Completo Match 3 Games Solver

8 Rainhas

O objetivo do problema das 8 rainhas é colocar 8 rainhas em um tabuleiro de xadrez de forma que nenhuma rainha consiga atacar outra. Observe que no xadrez uma rainha pode se movimentar na linha, em colunas e nas diagonais. Já existem soluções para esse problema, inclusive para a colocação de ‘n-rainhas’. Esse também é um problema brinquedo. 

Esse problema pode ser formulado de duas formas: a incremental e a completa. A formulação incremental diz que o estado inicial contém nenhuma rainha e cada uma é colocada sequencialmente. A formulação completa considera que as 8 rainhas começam no tabuleiro e podem se movimentar.

Observe que o custo é completamente ignorado independente de qual formulação é utilizada. O importante é o estado final. Uma formulação incremental possível é a seguinte:

• Estados: Qualquer posicionamento de 0 até 8 rainhas no tabuleiro.
• Estado inicial: Nenhuma rainha no tabuleiro
• Ações: Adicionar uma rainha em qualquer estado vazio
• Modelo de transição: Retorna o tabuleiro com a rainha adicionada em um espaço específico.
• Teste de objetivo: Todas as 8 rainhas estão no tabuleiro, e não conseguem se atacar.

Com essa formulação obtemos 64 * 63 * … * 57 o que equivale aproximadamente à 1.8 * 10 14 sequências possíveis para serem investigadas. Uma formulação melhor proíbe a colocação de uma nova rainha se um tile pode ser atacado.

• Estados: Todas as combinações das n rainhas (0 ⇐ n ⇐ 8), sendo que uma por coluna nas colunas n mais à esquerda, sem que nenhuma rainha ataque outra.
• Ações: Adicione uma rainha em qualquer célula na coluna mais à esquerda possível de forma que não seja atacada por uma outra rainha.

Com essa formulação o problema das 8-rainhas tem seu espaço de busca reduzido para apenas 2057 possibilidades. Entretanto, se considerarmos 100 rainhas a redução do espaço de busca é de 100400para 1052 o que é considerado um grande progresso, mas não suficiente para deixar este problema tratável.

A sequencia de Knuth

Esse problema foi apresentado pelo matemático e cientista da computação Donald Knuth em 1964 e ilustra como estados de busca podem crescer rapidamente. Knuth conjecturou que a partir do número 4 uma sequência de fatoriais, raízes quadradas e truncamentos pode alcançar qualquer número inteiro positivo. Esse é um outro exemplo de problema brinquedo.

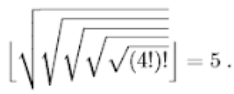
A definição deste problema é bastante simples:!

• Estados: Números positivos
• Estado Inicial: 4
• Ações: Aplicar uma operação de fatorial, raiz quadrada ou truncar (fatorial é apenas disponível para números inteiros)
• Modelo de transição: Dado pela definição matemática dessas operações
• Teste de Objetivo: O estado atual é o desejado.

Entretanto, não é conhecido um limite de quão grande um número é necessário para alcançar um determinado alvo, por exemplo, o número 620.448.401.733.239.439. 360.000 é um dos estados gerados pela expressão para 5. Portanto, o espaço de busca é infinito. Espaços de busca infinitos são comuns em tarefas que envolvem a geração de expressões matemáticas, circuitos, provas, programas ou ainda objetos que são definidos recursivamente.

Caixeiro Viajante

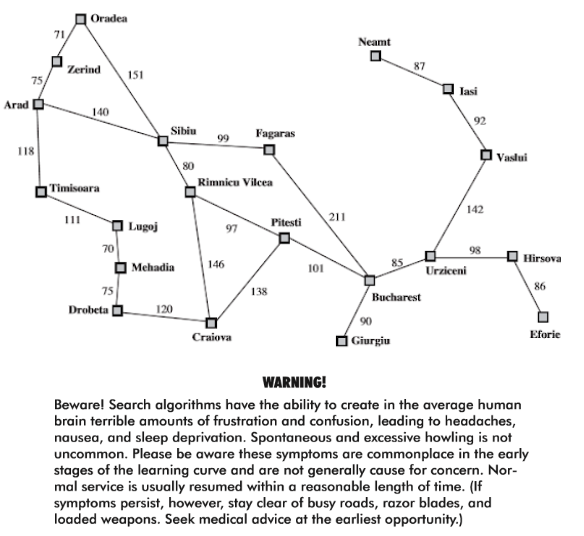
O problema do caixeiro viajante (TSP) é um dos problemas reais mais famosos da matemática e da computação. Esse problema foi inspirado na necessidade de vendedores realizarem entregas em diversos locais (cidades) percorrendo o menor caminho possível, reduzindo também o tempo e os outros possíveis custos com transportes e combustíveis. O problema do caixeiro viajante é a procura de um circuito que possua o menor custo possível, começando em uma cidade qualquer, entre as várias, e visitando cada cidade uma vez e regressando à cidade inicial.

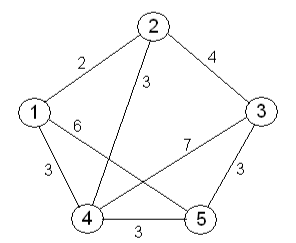
Matematicamente utilizando a interpretação de teoria dos grafos o problema do caixeiro viajante pode ser formulado como segue:

Cada cidade é identificada como um vértice e as rotas que ligam cada par de nós são as arestas. Cada uma destas linhas estão associadas à distâncias (custos) correspondentes. Se for possível ir de uma cidade para qualquer outra, diz-se que o grafo é completo. Uma viagem que passe por todas as cidades corresponde a um caminho Hamiltoniano que é representado por um conjunto de arestas. O custo total é igual ao somatório dos custos das arestas presentes no ciclo. “Um caminho hamiltoniano é um caminho que permite passar por todos os vértices de um grafo G, não repetindo nenhum, ou, seja, passar por todos uma e uma só vez por cada. Caso esse caminho seja possível descrever um ciclo, este é denominado ciclo hamiltoniano (ou circuito hamiltoniano) em G. E, um grafo que possua tal circuito é chamado de grafo hamiltoniano.” - Wikipédia 

A forma formal de formular esse problema é através de um grafo G(V,E) com V3e custos cij (i, j) Eque referentes às arestas do grafo. O objetivo, caso exista um grafo completo com n vértices é encontrar o melhor circuito entre os (n-1)!/2 possibilidades. Algumas instâncias desse problema também consideram o sentido das arestas entre os nós. O problema do caixeiro viajante é um problema NP-Completo.

Busca de rota (Pathfinding)

O problema da Busca de Rota (Pathfinding) é a busca feita para a menor rota entre dois determinados pontos. É uma variação mais prática para a solução de labirintos e é fortemente relacionado ao problema presente em teoria de grafos chamado de problema do menor caminho. Esse é um problema real e que teve uma grande contribuição feita pelo algoritmo de Dijkstra. O problema do pathfinding ainda é um problema não completamente resolvido para ambientes multiagentes, entretanto, existem muitas abordagens diferentes. 

Usaremos como exemplo de problema que pode ser resolvido por pathfinding: uma linha área que deve resolver o planejamento de uma viagem por um web-site.

• Estados: Cada estado obviamente inclui uma localização, um aeroporto, e o tempo atual. Por conta do custo da ação, o voo que o passageiro irá fazer entre um aeroporto e outro, é necessário cada estado também armazenar esse custo.
• Estado Inicial: O aeroporto que o cliente irá selecionar no site
• Ações: Pegar qualquer voo da localização atual, em qualquer assento e saindo no tempo atual. Deixando um tempo para a transferência do passageiro.
• Modelo de transição: O estado resultante de pegar um voo entre o aeroporto atual e o próximo, além de considerar o tempo entre as viagens.
• Teste de Objetivo: O aeroporto final é o escolhido?
• Custo: Depende do custo monetário, o tempo de espera, o tempo de voo, taxas, tempo no dia, horário do voo, do avião, da milhas do passageiro…

Essa é uma versão simplificada do problema e não são criados planos alternativos. Um bom sistema inteligente deve incluir planos de contingência que permitam a extensão considerando a probabilidade da falha e os novos custos.

Buscando soluções para estes problemas

Agora que já entendemos alguns problemas de planejamento é necessário buscar soluções para esses problemas. Uma solução pode ser definida como a sequência de ações necessárias para um obter um objetivo. Essa sequência de ações pode ser representada através de uma árvore de busca. Um árvore de buscas é construída utilizando o nó inicial como a raiz, os outros nós correspondem à estados possíveis presentes no espaço de busca e as arestas são as ações. Todos os nós disponíveis para expansão são chamados de fronteira ou lista aberta.

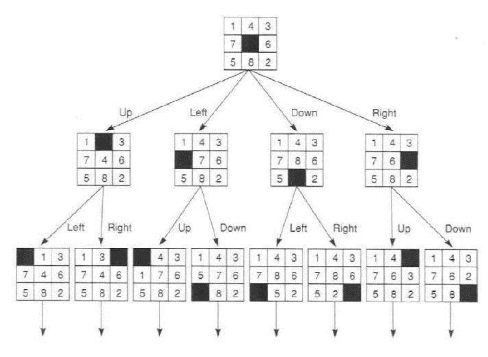
A essência da busca é seguir uma opção num instante e ignorando todas as outras para depois revisita-las, caso essa opção não leve a solução. O objetivo final é expandir a fronteira até encontrar um estado objetivo ou não que não existam mais estados para serem expandidos. No fim das contas, algoritmos de busca tem a mesma estrutura e variam primariamente me como eles escolhem qual estado para expandir.

Alguns problemas, existem estados que são redundantes e que podem levar a árvore infinita e portanto uma busca infinita. Em alguns casos é possível evitar redundâncias dependendo de como o problema é definido. Entretanto, em alguns problemas isso é impossível como nos puzzles em que uma ação é reversível ou ainda no pathfiding. Uma forma encontrada para evitar os caminhos redundantes é a utilização de uma estrutura de dados para guardar os estados já visitados: explored set (alguns autores também chamam de closed list). Para cada novo estado é verificado se ele pertence a esse conjunto, se sim ele é descartado automaticamente ao invés de serem adicionados na fronteira. A partir disso um novo algoritmo é gerado:

Por conta do algoritmo utilizado em buscas com grafos, a árvore de busca gerada terá pelo menos uma cópia de cada estado. Outra característica importante é a clara separação entre os estados visitados, a fronteira e os estados não explorados. 

Soluções de busca

Os critérios utilizados para comparar as soluções de algoritmos de busca criadas são: completude, otimização, complexidade de tempo e complexidade de espaço. A completude verifica se o algoritmo com certeza encontra a solução se ela existe. A otimização verifica se a estratégia utilizada encontra melhor solução. A complexidade de tempo verifica quantos passos são necessários para uma solução ser encontrada. Já a complexidade de espaço verifica o quanto é necessário de memória para fazer uma busca.

Algoritmos de Busca Cega  (Uninformed Search Strategies)

O termo busca cega identifica um grupo de estratégias de busca que utilizam nenhum tipo de informação sobre os estados, além das apresentadas na definição do problema. Os algoritmos de busca cega apenas verificam se os estados sucessores são um dos estados objetivos. As estratégias de busca são diferenciadas através da ordem em que os nós são expandidos. Qualquer estratégia que sabe determinar se um estado é mais promissor que outro é considerada uma busca informada ou ainda uma busca com heurística.

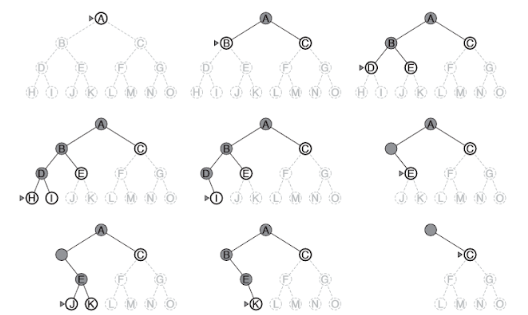
Busca em Largura

A busca em largura, também conhecido como breadth-first search, é uma estratégia bastante simples em que o primeiro nó é o expandido, e então seus sucessores são expandidos em sequência. Em geral, todos os nós são expandidos em uma determinada profundidade na busca, antes de se começar o processo de expansão do próximo nível. Para a construção dessa busca é utilizada uma fila para os nós da fronteira. Todos novos estados são colocados no final desta fila e os nós presentes neste nível.

Observe que este algoritmo segue como base um algoritmo de busca em grafos por manter um conjunto de estados visitados. O algoritmo básico é apresentado como:

• Completude: Se o estado objetivo mais superficial for de alguma profundidade finita d, o algoritmo de busca em largura irá eventualmente encontrar uma solução depois de gerar todos os nós mais superficiais. Assim que o nó objetivo for gerado, nós sabemos que este é o nó mais raso, já que todos os nós gerados foram testados e descartados. 

• Otimização: É necessário diferenciar que não necessariamente o nó objetivo mais raso é o nó objetivo ótimo, tecnicamente, o algoritmo de busca em largura encontra um caminho ótimo se o custo do caminho for uma função não decrescente da profundidade do nó. O cenário mais comum é que todas as ações têm o mesmo custo.

• Complexidade de tempo: Considere que está sendo feita uma busca em uma árvore uniforme e que cada estado tem b sucessores. O nó raiz irá gerar b estados no primeiro nível, cada um dos sucessores irá gerar mais b estados, portanto existem b2 estados no segundo nível. Em seguida, cada um destes nós geram mais b estados, obtendo assim b3. Supondo que a solução esteja na profundidade d o total de estados gerados são: b + b2 +b3+ … + bd =O(bd)

• Complexidade de espaço: Para qualquer busca em grafos que guarde cada vértice num conjunto de explorados, a complexidade de armazenamento sempre será em fator do valor de b. Para busca em largura em particular, cada nó gerado irá permanecer na memória, então sempre existiram O(bd-1)estados no conjunto explorado e O(bd) estados na fronteira. Como na computação nós sempre escolhemos o maior valor para determinar a complexidade de um algoritmo, então a complexidade de espaço é de O(bd)

Uma complexidade exponencial é bastante assustadora. Na tabela a seguir vemos o crescimento do uso de memória e tempo para diversos valores de d utilizando um valor de b=10. Nessa tabela assume-se que 1 milhão de estados podem ser gerados por segundo e que cada nó requer 1000 bytes de espaço.

A partir dessa tabela é possível concluir que o uso de memória da busca em largura é um problema grave se comparado ao tempo de execução. Academicamente falando, é possível que alguém espere por 13 dias por uma busca em profundidade ser executada, mas ninguém tem 1 petabyte de memória. Entretanto, também é importante notar que se a solução estiver na profundidade 16 irá levar 350 anos para o problema ser resolvido. Em geral, problemas de complexidade de busca exponencial não podem ser resolvidos por métodos de busca cega até mesmo para pequenas instâncias.

Busca Uniforme (Uniform-cost search)

Quando todos os custos das ações são iguais, então o algoritmo de busca em largura é ótimo já que sempre alcança o nó mais raso da árvore. Com uma simples expansão é possível sempre encontrar o melhor caminho independente de qual é a função custo utilizada. Ao invés de expandir o nó mais raso, a busca uniforme busca expandir o nó n que tenha o menor custo de caminho dado pela função custo g(n). Isso é feito utilizando uma fila de prioridade ordenada por g.

Além de ordenar essa fila utilizando o custo do caminho como referência, existem outras duas diferenças significativas com relação à busca em largura. A primeira diferença é que o objetivo teste é aplicado ao nó quando ele é selecionado para a expansão ao invés de ser utilizado quando ele é gerado. O motivo dessa escolha é que é possível que esse objetivo resultado seja um resultado sub-ótimo. Outra diferença é que feito um outro teste considerando caso exista um novo estado com um custo melhor na fronteira.

Otimização: É fácil ver que a busca uniforme é ótima em geral. Primeiro, ela sempre seleciona para investigar um estado n, o melhor custo é sempre o selecionado. Como o custo nunca é negativo, então o caminho não pode ficar mais curto que o pré-definido. Por esses dois motivos, a busca uniforme sempre expande o caminho utilizando uma ordem ótima.

Completude: A busca uniforme não se importa com o número de passos o caminho contém, apenas com o custo total. Por essa característica, se existir uma possibilidade de uma sequência de custo zero infinita, por exemplo de alguma forma a ação selecionada seja justamente “não fazer nada”. A completude é garantida se o custo de cada ação for maior que uma determinada pequena constante positiva.

Complexidade de tempo e memória: Considere C* como o custo ótimo da solução encontrada e assuma que cada ação tem ao menos um custo de . Então a complexidade no pior caso é O(b1+C*/)o que pode ser muito maior que bd. Esse custo é justificado pelo fato que a busca uniforme explora árvores maiores com passos menores antes de buscar em passos maiores que podem ser mais úteis. Observe que se todos os custos forem iguais então (b1+C*/ é igual à bd+1. Quando todos os custos são iguais essa estratégia tem um comportamento bastante similar à busca em largura, exceto que ela irá não irá parar assim que encontrar o estado objetivo.

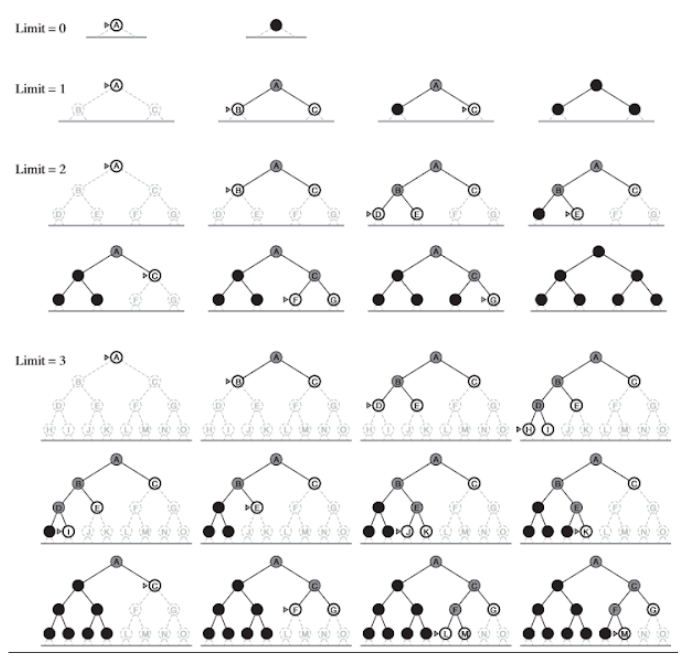
Busca em Profundidade

O método de busca em largura sempre busca expandir o estado mais profundo da fronteira da árvore de busca. A busca sempre procede para o nível mais profundo da árvore de busca até que os nós não tenham mais sucessores. Assim que os nós são expandidos. Assim que os nós são expandidos, eles são removidos da fronteira e a busca recomeça no próximo nó mais profundo que ainda tenha estados alcançáveis.

A busca em profundidade utiliza uma pilha ao invés de utilizar uma fila como a busca em largura utiliza. Isso significa que o estado mais recentemente gerado será o escolhido para a expansão. Este deverá ser o nó mais profundo na árvore já que é pelo menos um nível mais profundo que o nó pai (que originalmente era o nó mais profundo).

• Completude: A implementação da busca em profundidade é bastante dependente da implementação correta da busca em grafos, já que com a busca em grafos estados repetidos são ignorados. Evitando caminhos redundantes a busca em grafos irá eventualmente expandir cada estado presente. Observe que se for utilizada uma implementação baseada em busca com árvores a busca em profundidade não é completa. A busca em profundidade pode ser modificada de forma que verifique se os novos estados contra os caminhos anteriores da raiz até o nó atual, sem ter nenhum custo de memória. Observe que se o estado de busca for infinito, ambas as versões irão falhar se não encontrado um caminho não finito entre o estado inicial e o objetivo.
• Otimização: Independente da versão utilizada, ambas as versões são não ótimas. Considerando a árvore de busca apresentada, se o nó objetivo fosse o J ou o C, a busca em profundidade iria encontrar o nó J primeiro antes de encontrar o nó C. Portanto, a busca em profundidade não é ótima
• Complexidade de tempo: A busca em profundidade poderá gerar um total de O(bm)nós, onde o m é a profundidade máxima de cada nó. Esse valor pode ser muito maior que o espaço de busca. Observe também que m pode ser muito maior que d ou ainda infinito se a árvore não tiver nós folhas.
• Complexidade de espaço: A vantagem da utilização da busca em profundidade ao invés da busca em largura é uma complexidade de espaço menor. Para a buscar em um grafo a busca em profundidade necessita apenas armazenar um único caminho da raiz até o estado objetivo. Assim que um nó é expandido, ele poderá ser removido da memória, assim que todos os seus filhos forem explorados. Ou seja, para um espaço de busca com ramificação de fator b e profundidade máxima de m, a busca em profundidade requer apenas O(bm) nós.

Utilizando os mesmos dados de entrada da tabela de complexidade da busca em largura, descobre-se que a busca em profundidade utiliza apenas 156 kilobytes em comparação com os 10 exabytes na profundidade 16, ocupando assim 7 trilhões de espaço a menos. Por esse comportamento, é comum que a busca em profundidade seja a primeira escolha em muitas áreas da IA.

Busca em Profundidade Limitada

A falha da busca em profundidade em espaços de busca infinitos pode ser aliviada se determinarmos um limite máximo de profundidade para a exploração l. Ou seja, os nós na profundidade l são tratados como se não existissem mais sucessores. Essa abordagem é também chamada de busca em profundidade limitada.

• Completude: Com a adição dessa profundidade limite, nós adicionamos a possibilidade de incompletude se o estado objetivo estiver mais profundo do que o pesquisado até então.
• Otimização: Observe que a busca em profundidade também não é ótima para casos em que l > d.
• Complexidade de tempo: O(bl)
• Complexidade de espaço: O(bl)

Algumas vezes o valor de l pode ser determinado através do conhecimento sobre o problema sendo resolvido. Por exemplo, no mapa da Romênia existem 20 cidades, é impossível a formação de um caminho com mais de 19 visitas. Essa seria a primeira escolha, entretanto, se observar com atenção o mapa é possível observar que é possível chegar de qualquer cidade a outra com apenas 9 passos, então o ideal é utilizar l = 9.

Busca com Aprofundamento Iterativo

A busca com aprofundamento iterativo é uma estratégia comumente utilizada junto com a busca em profundidade limitada. A busca é feita aumentando de maneira gradual o limite até que o objetivo é encontrado. A vantagem é que na busca com aprofundamento iterativo as qualidades da busca em largura e da busca em profundidade são combinadas. Ela é completa e ótima como a busca em largura e é modesta quanto a complexidade de memória: O(bd).

A busca com aprofundamento iterativo pode ser vista como “gastadora” já que gera os estados possíveis múltiplas vezes. Entretanto, na realidade, não é tão custoso assim. Como mostrado anteriormente, o grande custo é a geração dos nós mais profundos da árvore. Nesse método os nós com profundidade d são gerados uma vez, os estados com profundidade d-1 são gerados 2 vezes e assim por diante. Portanto, a raiz é gerada d vezes. Então, os nós são gerados no pior caso: N(IDS) = db + (d-1)b2 + … +1bd!

Como na computação sempre definimos como a complexidade o “maior valor” então obtemos uma complexidade de tempo de O(bd)que é a mesma complexidade da busca em largura. A busca com aprofundamento iterativo é o modo de busca preferido caso exista um espaço de busca muito grande ou se a profundidade da solução for desconhecida.

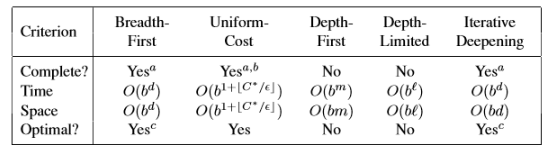
Comparando Métodos de Busca Cega

A tabela a seguir mostra a comparação entre os métodos de busca apresentados utilizando a abordagem utilizando árvores. Para buscas utilizando grafos a principal diferença é que o método de busca em profundidade é completo se for considerado um espaço de busca finito e o espaço e o tempo necessários são proporcionais ao tamanho do espaço de busca. Observe que b é o coeficiente de ramificação da árvore utilizada; d é o nível mais raso em que a solução se encontra; m indica a profundidade máxima da busca; l indica o limite de profundidade; O sobrescrito a indica é completo apenas se o espaço de busca for finito; b completo se o custo do passo for para um positivo ; c ótimo se o custo dos passos forem idênticos;

｡･:*:･ﾟ★,｡･:*:･ﾟ☆ ｡･:*:･ﾟ★,｡･:*:･ﾟ☆ ｡･:*:

Contact Info:

E-mail: pamabeltrani@gmail.com

Discord: pamnawi